この記事は Akatsuki Advent Calendar 2018 - Adventar 1日目の記事です。
はじめに
こんにちは。クライアントエンジニアのRiyaaaaaです。
皆さんは最近シェーダーを書いていますか? 私はあんまり書いていないですね。
長らく触れないと、カンが鈍りがちになりますよね。なので、定期的に簡単なものでも書いたり作ったりすることは脳の体操にも効果的です。
しかし、いざシェーダーを書こう!と思っても、ゲームエンジニアにとってはシェーダーはゲームやレンダラーと密接に結びついていて、手軽に何かを試すというのは難しかったりします。UnityやUnreal Engine4をわざわざ起動するのも億劫ですよね。
そんな時、GLSL(OpenGL Shading Language)をWeb上でコーディングできるサービスがオススメです。有名なところだとGLSL Sandbox GalleryやShadertoy BETAですね。
今回はGLSL Sandbox Galleryを使った、リアルタイムアニメーションCG(デモシーン)の作成の流れを紹介しようと思います。
この記事で皆さんが手軽にGLSLを触るようになり、レイマーチングをはじめとするリアルタイムレンダリングに興味を持っていただければ幸いです。
GLSL Sandboxの基本
このサイトは、ピクセルシェーダーをリアルタイムにコーディングできるサイトです。こちら使い方は非常にシンプルで、GLSLを記述するとリアルタイムに変更が背景に反映されます。基本的な仕様は以下となります。
・gl_FragCoordに現在処理の対象となっているピクセルの座標が二次元ベクトルとして定義されます。 (定義域:(0, 0) ~ (xの解像度、yの解像度))
・gl_FragColorにそのピクセルの色をRGBAの4次元ベクトルで設定します。(値域:(0, 0, 0, 0) ~ (1, 1, 1, 1))
試しに、gl_FragColorにRGB成分が全て0.5のベクトルを代入してみましょう。
// floatの精度を指定します precision mediump float; uniform float time; uniform vec2 resolution; uniform vec2 mouse; void main( void ) { gl_FragColor = vec4(0.5, 0.5, 0.5, 1.0); }
GLSL Sandboxでは3つのuniform変数が使えます。timeは経過時間、resolutionはウィンドウの解像度、mouseは現在マウスがフォーカスしている座標です。mouse、resolutionはgl_FragCoordと同じ定義域を持ちます。
このコードでは座標(gl_FragCoord)に関わらず一様に(0.5, 0.5, 0.5)の色を代入しているので、画面は全て灰色に染まることでしょう。また、数字を変化させるとリアルタイムに背景の色が変わって行くのがわかると思います。
次に、座標を色で表してみます。ここで、座標(gl_FragCoord)は(0, 0)からresolution.xyの値をとりますが、色は0から1で指定しなくてはならないので、座標を0 ~ 1で正規化しましょう。
// 省略 void main( void ) { vec2 p = gl_FragCoord.xy / max(resolution.x, resolution.y); gl_FragColor = vec4(p, 0.0, 1.0); }
main関数を上記のように書き換えると、こんな画面が描画されることと思います。

R, G成分をX, Y座標に対応させているので、右に行けば行くほど赤く、上に行けば行くほど緑に近づいていきます。(縦横比が違う場合、厳密には短い方は0~1で正規化はできていません)
GLSL Sandboxの基本的な解説は済んだので、本題のレイマーチングをこのGLSL Sandboxの上で実装してみましょう。
レイマーチングの基本
レイマーチングとは、広義のレイトレーシングの一つです。カメラからレイを飛ばし、色を決定するところまでは同じですが、レイマーチングではレイの交差判定に距離関数というものを使います。距離関数とは、ある集合の中の二点の距離を定義する関数です。もっとも有名なのはユークリッド距離関数で、一般的な人間の感覚における「距離」を示す関数です。ユークリッド距離関数は距離関数の一つですが、ユークリッド距離関数 ≠ 距離関数であることには注意しましょう。
つまり、レイマーチングは語弊を恐れずいうならば、全てのピクセルについて、シーン上に存在するオブジェクトを示す距離関数のどれかが0を返すまでレイを飛ばし(もしくは定められた計算数まで)、ヒットしたオブジェクトを描画する手法です。

実際に書いてみましょう。
// 球の距離函数 float sphere_d(vec3 p) { const vec3 sphere_pos = vec3(0.0, 0.0, 3.0); const float r = 1.0; return length(p - sphere_pos) - r; } struct Ray { vec3 pos; vec3 dir; }; void main( void ) { // 画面座標の正規化。中心が(0, 0)の方が都合がいいため-1 ~ 1で正規化する vec2 pos = (gl_FragCoord.xy * 2.0 - resolution) / max(resolution.x, resolution.y); // カメラの位置。中心から後方にあるイメージ vec3 camera_pos = vec3(0.0, 0.0, -4.0); // カメラの上方向の姿勢を定めるベクトル この場合水平 vec3 camera_up = normalize(vec3(0.0, 1.0, 0.0)); // カメラの向いている方向 vec3 camera_dir = normalize(vec3(0.0, 0.0, 1.0)); // camera_upとcamera_dirの外積から定まるカメラの横方向のベクトル vec3 camera_side = normalize(cross(camera_up, camera_dir)); // レイの位置、飛ぶ方向を定義する Ray ray; ray.pos = camera_pos; ray.dir = normalize(pos.x * camera_side + pos.y * camera_up + camera_dir); float t = 0.0, d; // レイを飛ばす (計算回数は最大64回まで) for (int i = 0; i < 64; i++) { d = sphere_d(ray.pos); // ヒットした if (d < 0.001) { break; } // 次のレイは最小距離d * ray.dirの分だけ進める(効率化) t += d; ray.pos = camera_pos + t * ray.dir; } if (d < 0.001) { // ヒットしていれば白 gl_FragColor = vec4(1); } else { gl_FragColor = vec4(0); } }
スフィア一個を配置し、カメラを画面後方に設定しました。位置関係を図で表すと以下のような感じです。
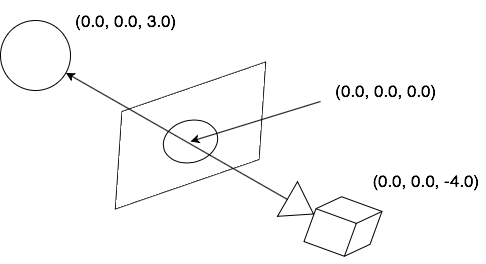
そして、以下のように描画されます。

これで最も基本的なレイマーチング は実装できました。しかし、せっかく3Dでやっているのに平べったく見えてしまいます。
次はライティングをしてみましょう。
レイマーチングにおけるライティング表現
今回はディレクショナルライトによるライティングを行います。必要なのは、光源ベクトルと、ライティング対象の法線ベクトルです。
一般的な3Dのレンダリングにおいては、法線ベクトルは頂点データから与えられますが、レイマーチング の場合は距離函数による衝突判定を行っているため、同じの手法は使えません。
ここで、数学的なアプローチにより、「陰関数の勾配ベクトルは法線ベクトルとなる」という性質を使って、法線ベクトルを求めてみたいと思います。
勾配ベクトルとは、各成分の偏微分を並べたベクトルを指します。陰関数とはの形で表される関数のことを指し、距離函数も陰関数表示の一つです。
つまり、距離函数を使って任意の座標の法線ベクトルを求めるためには
を求める必要があります。xの偏微分の定義は以下。
y, zの偏微分についても同様のことが言えます。
数値計算的に求めてみましょう。
vec3 sphere_normal(vec3 pos) {
float delta = 0.001;
return normalize(vec3(
sphere_d(pos + vec3(delta, 0.0, 0.0)) - sphere_d(pos),
sphere_d(pos + vec3(0.0, delta, 0.0)) - sphere_d(pos),
sphere_d(pos + vec3(0.0, 0.0, delta)) - sphere_d(pos)
));
}
これで法線ベクトルを求めることができます。
次に光源ベクトルをLとして、頂点の輝度を求めましょう。ここではシンプルにランバート反射を使います。
vec3 L = vec3(0.0, 0.0, 1.0); // 光源ベクトル vec3 N = sphere_normal(ray.pos); // 法線ベクトル vec3 LColor = vec3(1.0, 1.0, 1.0); // 光の色 vec3 I = dot(N, L) * LColor; // 輝度
これらを先ほどの実装に組み込むと、このようにライティングされます。

ソースコードが長くなってしまったので、フルバージョンはgistにアップしています。
raymarching-sphere-lighting · GitHub
光源ベクトルが(0.0, 0.0, 1.0)なので、球の正面に光を当てていることになりますね。光の方向を変えてみると光の当たり方が変わります。(必ずその際は光源ベクトルを正規化をしてください)
他にも、距離函数にmod関数(剰余)をかますことで、レイの値域を制限し、あたかもオブジェクトが複製されているように見せかけるテクニックがあります。
float sphere_d(vec3 p) { const float r = 1.0; return length(mod(p, 4.0) - 2.0) - r; }

さて、ここまで基本を抑えてしまえばあとはなんでもありです。
超かっこいいエフェクト(ブルームや走査線など)を好き放題追加するのもありですし、面白い距離函数を実装してみるのもいいかもしれません。
最後に、パーリンノイズを使ったレイマーチング によるテライン描画をやってみましょう。
パーリンノイズを使ったレイマーチングによるテライン表現
パーリンノイズは、テクスチャの表現によく使われる、とても自然に感じる(?)擬似乱数を生成するアルゴリズムです。話すと長くなるのでここでは端折って、解説や実装を引用したいと思います。
今回はこの中にあるパーリンノイズをさらに改良したシンプレックスノイズというのを使いましょう。このシンプレックスノイズを、距離函数として応用してレイマーチングに使用します。
試しにまず、このシンプレックスノイズをテクスチャとして描画してみましょう。
void main( void ) { vec2 pos = (gl_FragCoord.xy * 2.0 - resolution) / max(resolution.x, resolution.y); // snoiseは上記文献で示されているシンプレックスノイズ関数 float c = snoise(pos * 5.0); gl_FragColor = vec4(c, c, c, 1.0); }

この時、シンプレックスノイズ関数は、という二変数関数で示される曲面であると解釈できます。(数学でよく表す空間と、GLSLの空間ではzとyが逆転していることに注意してください)
つまり、レイの座標を(Rx, Ry, Rz)とすると、 を満たすとき、レイはこのシンプレックスノイズ曲面上にある(衝突した)と考えることができます!
float map(vec3 v) { // 地面のオフセット const float GROUND_BASE = 1.2; return v.y - snoise(v.xz * .4) + GROUND_BASE; } vec3 map_normal(vec3 v) { float delta = 0.01; return normalize(vec3(map(v + vec3(delta, 0.0, 0.0)) - map(v), map(v + vec3(0.0, delta, 0.0)) - map(v), map(v + vec3(0.0, 0.0, delta)) - map(v))); }
謎のマジックナンバーが出てきていますが、これは自由に変えることが可能なパラメータです。試しにいじってみるのもいいでしょう。
さて、このmap関数をスフィアの距離函数の代わりに使い描画してみると...
raymarching-terrain-sample · GitHub

見事テラインが描画されました! 今回は、カメラの座標にtimeを加えているので、リアルタイムにテラインが動いていくのがわかると思います。
おわりに
レイマーチングは解説した通りレイトレーシングの交差判定に距離函数を使うだけのシンプルなアルゴリズムです。一方で、その応用範囲は無限大です。距離函数はその特性上、幾何的なオブジェクトの描画に向いていますが、組み合わせや微調整を繰り返すことで、生き物のようなオブジェクトを描画することだって可能です。ボリュームレンダリングという3次元的な広がりのあるデータの描画に応用して雲などを描画することもできます(こちらは、実際に多くのゲームへの採用例があります)。
他にも、パーリンノイズによるテライン表現を応用すると、グランドキャニオンのような光景や、リアルな水面でさえも描画することができます。
このように、レイマーチング等を用いたデモシーンは、様々な工夫や自分の考えた最強の関数などを好き放題盛り込んで一つの作品を作る面白い分野です。ぜひ遊んで、あなただけの作品を作ってみてください。